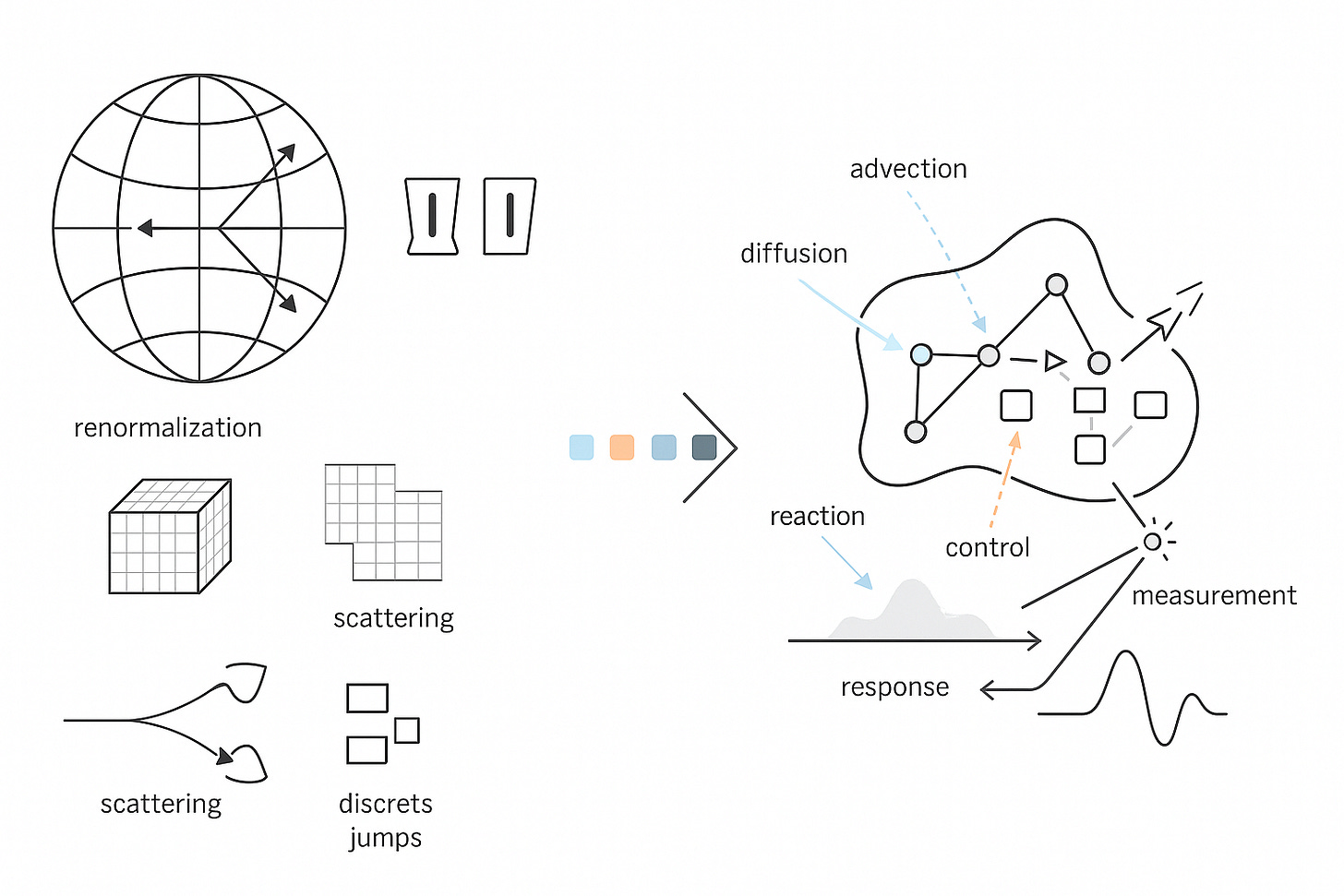
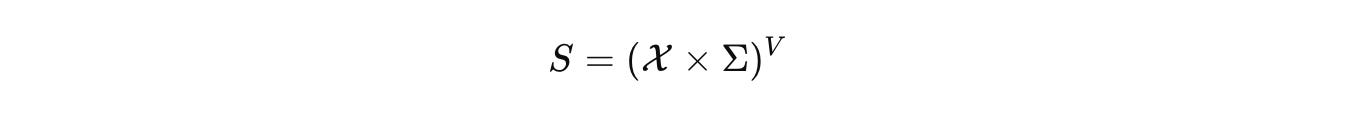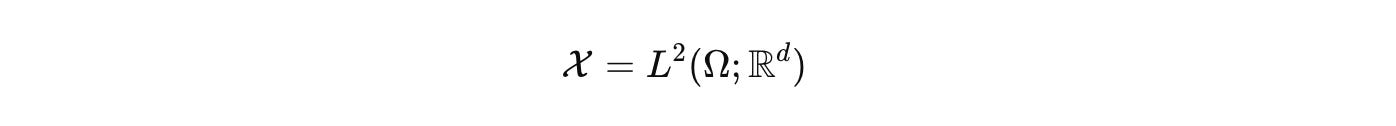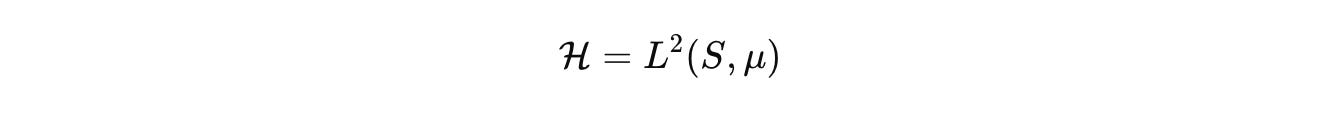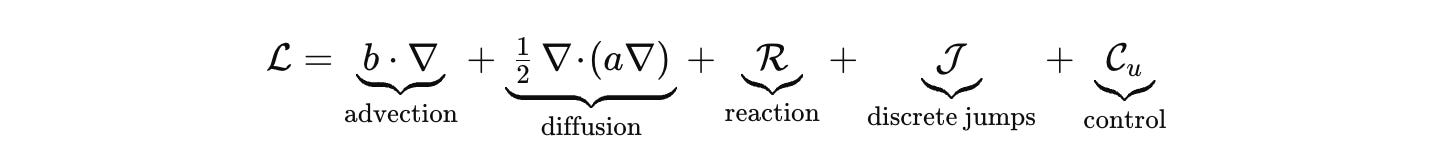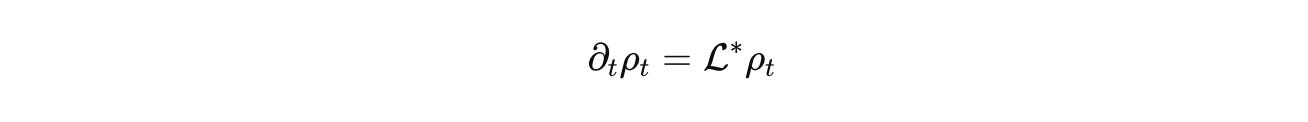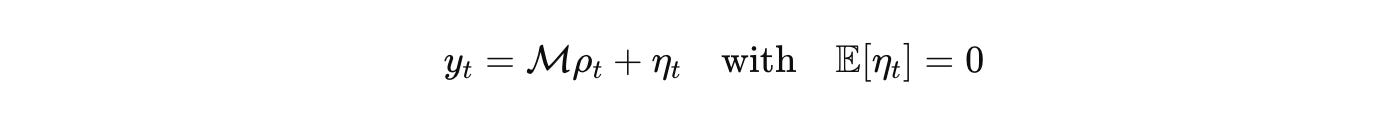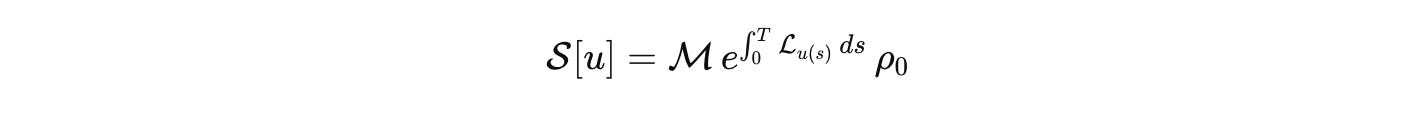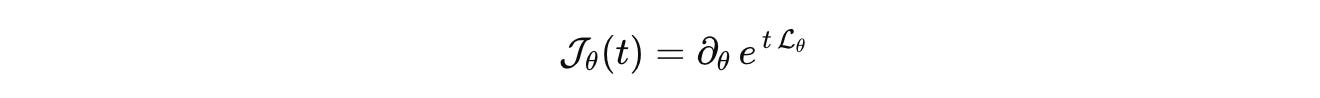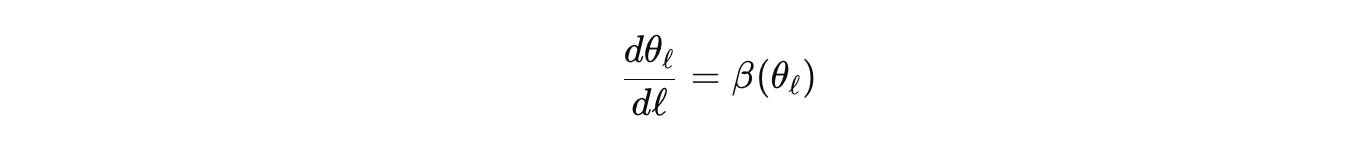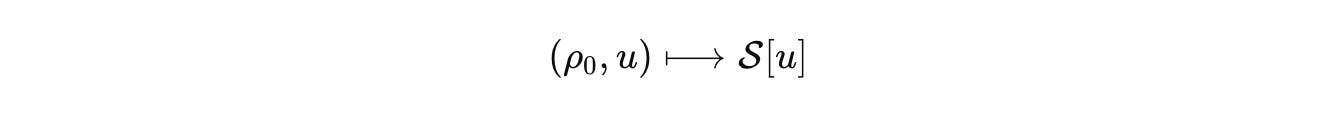A Universal State Space for Living Systems
Physics earned prediction through Hilbert space and operator algebras; Can we do the same for biology?
Physics became powerful when it chose discipline over description. It wrote down a state space, fixed the operators that act on it, and specified how measurement works. That choice, the Hilbert space with its operator algebra and a single generator for dynamics, bought us prediction with units attached, comparison across laboratories, control laws that survive contact with reality, and devices that work on the first principles they claim to use. The end goal was never a slogan about understanding nature. It was a compact calculus that lets us compute the outcome of an experiment, trade uncertainties honestly, and compose systems without breaking causality or units. Hilbert space carried the states. Self-adjoint operators carried the observables. A generator carried time. Renormalization taught us how parameters flow with scale and where the error goes when we coarse-grain. BRST and gauge fixing told us which parameters were real and which were bookkeeping. Scattering theory turned difficult dynamics into a currency of comparison that any competent lab could cash in a detector.
Biology deserves the same rigor. CELL is our commitment to it. At CELL, we want to build the single, comprehensive mathematical configuration at a given scale for biology. As a hypothesis, we start by naming the configuration space that actually carries biological state. Not a vague diagram, a space with measure and boundary. Let Ω be a tissue domain with boundary conditions. Let V index cells or compartments. Let Σ hold discrete internal modes such as promoter states or cell-cycle phases.
The hybrid configuration is
with
for the fields we care about, concentrations, voltages, stresses. We then work in the functional state space
where μ is the product of Lebesgue, counting, and graph measures. Dynamics are generated by a sectorial operator that respects budgets and geometry. Keep the palette explicit.
Advection and diffusion live where they belong, on Ω or on a graph that represents contact. R encodes stoichiometric chemistry with correct units. J handles discrete jumps such as promoter switching or fate change. C_u injects inputs, light pulses, drugs, mechanical stimuli. Densities evolve by the forward equation
Measurement is an operator with a noise model. Imaging, RNA-seq, ephys, proteomics appear as bounded linear functionals plus noise
Once these pieces are fixed, the outcome of a well-posed perturbation is a response operator
This is our biological analog of the S-matrix. It is the comparison currency across labs. Publish the state space, the generator, the measurement map, the input basis, and the error budget. Then models can be compared, falsified, and composed without translation errors masquerading as science.
What does this buy us when we stop hedging and adopt the operator view? Consider a simple, real experiment. A promoter toggles between off and on. mRNA diffuses in a dendritic spine with flux at the neck. You modulate the on-rate with a light pulse, short and square. In the generator, that is a change in a single rate inside the jump block, plus diffusion on the tissue domain. The measured fluorescence is the action of the measurement operator. Fit the pulse response, not a cartoon.
If this sensitivity operator is full rank on the input basis you chose, the rates are identifiable. If it is not, no amount of post hoc rhetoric will make them so. Change the input, change the sensor, or change the model class. That is the honesty physics forced on itself, and it is the honesty biology needs.
Take a second case that usually invites hand-waving. Adaptive cancer therapy with oxygen and ATP budgets. Write down the transport and consumption fields on the tissue domain. Place proliferation inside the reaction block. Let drug dose enter through the control block. Put toxicity and dose limits into the admissible control set. Now the design problem is clear. You are shaping the spectrum and pseudospectrum of the driven generator to keep growth modes suppressed while staying within budget. Small-signal analysis gives Kubo-style linear response around a background. Large-signal schedules come from optimal control on semigroups with inequality constraints. Either way, you compute a policy and a bound on what you cannot do, given biology’s budgets.
Or look at morphogenesis on a cellular graph. The adjacency enters through a Laplacian or a nonlocal kernel. Reaction terms come from a Jacobian that respects stoichiometry. Pattern selection and stability are spectral questions of a block operator that couples transport on the graph with the reaction block. Coarse-grain by graph contraction and spatial averaging to get an effective generator on a simpler domain. Track parameter flow with scale
and carry the error forward. If a wavelength appears in the coarse model that is forbidden by the fine model’s budgets, the derivation is wrong. The formalism itself tells you, instead of a reviewer six months later.
The end goal matches physics point for point. A compact state space where all admissible states live. A small generator palette that closes under composition and respects units. A measurement calculus that turns data into operators and operators into predictions. A renormalization story that quantifies what is lost and what is kept as we pass from gene to cell to tissue. A quotient that identifies parameters that matter and discards the rest. With that, reproducibility is not a campaign. It is a property of publishing the right objects. Engineering becomes possible in operator space. Control policies and assay designs are synthesized with the same confidence that gave electronics and lasers to physics.
Machine learning fits inside this, not above it.
Neural operators and kernel machines can learn that map under operator constraints. Train with spectral penalties and budget priors so the surrogate respects stoichiometry, positivity, and stability. Then it generalizes across tissues because the invariants are in the generator, not in the dataset.
When a learned model violates a budget, the violation is meaningful because the conservation law was carried by the generator or by a small slack. That is how we keep black boxes honest.
This is the wager. If we fix the state space and the operator calculus for biology, we buy the same things physics bought. Prediction with units and uncertainty. Comparison without translation fights. Control that does not collapse on contact with a new tissue. A shared response currency that lets two labs argue about science instead of file formats. A path from model to device, from model to therapy schedule, from model to assay choice, all inside a calculus that tolerates scrutiny and trades in numbers rather than adjectives.
Come build this with us at CELL. We are now on-boarding founding member labs and founding members to shape the narrative at CELL.
To apply send a mail to science+collaborate@cellbiosf.org
Substack: https://cellbiosf.substack.com
CELL is an open science consortium forging an aggressive mathematical core for biology. We fuse mathematical biology, biophysics, and computational biology to build, test, and openly share equations that predict and steer living systems.